連続する3整数を,中央の数をnとするとして表しなさい。 (3) (2)のとき,「連続する3整数の和は3の倍数である」ことを,文字を使って説明しなさい。 (2) 「偶数と奇数の積は偶数である」ことを,文字を使って説明しなさい。 3 2けたの整数 (十の位の数がa,一の位文字式による説明をするときは、問題文を利用すれば大丈夫です。問題文から 「対象」「計算方法」「結論」 を抜き出しましょう。 実践問題①連続する $\textcolor{green}{3}$ つの整数の和は $\textcolor{green}{3}$ の倍数であることを説明しなさい。 「対象」:連続する $\textcolor{blue}{3}$ つの整数具体的に数字を言ってみればわかりやすいかも! 例えば13,14,15 の中には当然偶数である2の倍数や、3個に一回入る3の倍数が含まれています。 同様に5個連続した整数の中には、5個に1つは5の倍数が含まれています。 また、ーは5個連続した整数なので5の倍数ですが、同時に3個連続した整数が

高校数学a 連続する整数の積 の性質 映像授業のtry It トライイット
連続する3つの整数の和は3の倍数である
連続する3つの整数の和は3の倍数である-連続する整数の和について,次の問いに答えなさい。 ① 次の文は,連続する3 つの整数の和が必ず3 の倍数になることを説明したものである。 ア ~ ウ にあてはまる式をそれぞれ答えなさい。中1数学・文字式の利用〜3つの連続する整数の和が3の倍数であることの証明 中 1 数学の「文字式の利用」で「3 つの連続する和」に関する 文章題 があります。 命題 3 3 3 つの連続する整数の和は 3 3 3 の倍数になる。 中 1 数学の中間・期末試験ではこの




赤点脱出シリーズ 捨てている人 損です 式による説明問題の解き方 コツさえ分かれば楽勝 夏期講習 生駒市 奈良市の個人契約 家庭教師しゅ 先生
N個の整数のうち、M個を選んで和を取ると、 N C M 通りの値が得られます。 この値からもとのN個の整数を求めるタイプの問題と、その亜流として差もとる問題を紹介します。 また、5+6+7=18 のように、連続する整数の和に関する問題もあわせてこのグループで紹介します。 同様に,\ 連続する3つの整数2,\ 3,\ 4の和は234=9なので3の倍数である 数学の証明問題では,\ 特定の場合にのみ成り立つことを示すだけでは不十分である1,3,5のように連続する3つの整数の中には、必ず3の倍数があることを示せ。 この問題を教えてください。 整数をn (n1) (n2)とおいたりするわけではないのですか? 数学a 連続する3つの整数 整数の
連続する3つの自然数の和は3の倍数である ことのほかに分かることがあります。下のアからオの中から1つ選びなさい。 ア 連続する3つの自然数の和は奇数である。 イ 連続する3つの自然数の和は偶数である。 ウ 連続する3つの自然数の和は最も小さい数の3連続する3整数に3の倍数が必ず1個含まれますので、連続する6整数なら前半3個のうち1個が3の倍数、後半3個のうち1個が3の倍数で、全体では3の倍数が2個となります。 連続する3整数に3の倍数が必ず1個含まれることは、連続する3整数の先頭の数を3で割った余りで場合分けすると math3n,\ 3n1,\方程式文章題 (連続する整数) 整数は1ずつ大きくなるので、xの次はx1である。 連続する3つの整数があり、その和は21である。 この3つの整数を求めよ。 If playback doesn't begin shortly, try restarting your device Videos you watch may be added
連続する3 つの整数のうち, 中央の整数をm とすると, したがって, 連続する3 つの整数の和は。3 の倍数である, 1 平均通過率729% 2 平均通過率384%1 無解答率75% 2 無解答率321%連続する3 つの整数をm-1,m,m+1と表す。 ( ただしm は整数とする)(m-1)+m+(m+1)=3mここで、mは整数なので3m は3 の倍数である。文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく 中3数学 2次方程式の文章題2 整数 練習編 映像授業のtry It トライイット 例題34は連続する3つの整数の積が6であることを証明しなくて良いのですか Yahoo 知恵袋 中学



2




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく
(mは整数) 2m* (2m1)* (2m2)=4m (2m1) (m1)ー① ①より連続した3つの整数の積は2の倍数ということが分かりますー② また連続した3つの数字じは少なくとも一つは3の倍数になるー③ よって、連続した3つの整数の積は②③より2の倍数でかつ3の倍数なので6の倍数になります。真ん中の整数をnとすると、 連続する3つの整数は、 n-1、n、n+1と表される。 その和は (n-1)+n+(n+1) =n-1+n+n+1 =3n nは整数だから、 3nは3の倍数 よって、連続する3つの整数の和は 3の倍数である。 この2人の説明は、どちらも正しい説明です。問題4 「連続する2つの奇数の和は4の倍数になる」 例3+5=8 このことを説明しなさい。 13+15=28 (わからない人は中2のワークp25 を参考にすること) 〔解答〕 nを整数とすると、連続する2つの奇数は2n-1,2n+1と表すことができる。




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく



Http Air M Study Jp Contents Pdf 3shikij Pdf
(課題) 連続する3つの整数の和は3の倍数であることを説明しなさい。 +2+3=6 5+6+7=18 だから、連続する3つの整 数の和は3の倍数になる。 さん 連続する3つの整数を、 n、n+1、n+2(nは整数)とす ると、それらの和はJ6 連続する3つの整数で、最大の整数の2乗が他の2数の積より16大きいとき、次の問いに答えなさい。 (1)最小の整数をxとして、xについての方程式をつくりなさい。 (2)この連続する3つの整数を求めなさい。 J7 連続する3つの整数がある。この3つの整数の和は、n+n+1+n+2=3n+3となる。 nは整数なので、3n+3は3の倍数である。 よって、連続する3つの整数の和は3の倍数となる。 別解 連続する3つの整数を n-1 、 n 、 n+1 とし




連続する3つの整数の和は3の倍数 もののはじめblog



1
亘:は整数であるから,3(二亘)は3の倍数である0 したがって,連続する3つの整数の和は3の倍数になる。 間2 間1の説明の二重下線部から「連続する3つの整数の和は3の倍数になる」ことの 他にわかることを,次のア~工の中から1つ選び,記号で答え 連続する3つの整数についての説明 問題は、2,4,6のように、一つおきに並んでいる整数の和は、3の倍数であることを説明しなさい。 n (n2)とんで (n4)なのか、解りません。 そもそも3の倍数は、6,9じゃないのですか? 4は入らないのではないですか?1 連続する3 つの3 の倍数の和は,9 の倍数であることを説明せよ。 2 連続する5 つの自然数の和は,5 の倍数であることを説明せよ。 3 「4 でわると1 余る数と4 でわると3 あまる数の和は4 の倍数である」ことを説明せよ。 中2数学 式の計算 式の説明② 氏名



2



Q Tbn And9gcsj032wcr 6cnslcx5wupxgh7s0hmxa00qycwq7lsonp0ubhpos Usqp Cau
連続する3 つの整数の和はア のイ 倍である。Q1 連続する2つの整数の平方の和は奇数である。 Q2 連続する3つの整数の立方の和は3の倍数である。 Q3 x+y=1の時(x2乗+y)2乗=(y2乗+x)(1ーxy) Q4 abc=0の時,a3乗+b3乗+c3乗=3abc お願いします。教えてください。「連続する3つの整数において、最も大きい整数とまん中の整数の積から最も小さい整数の2乗をひいた数に1をたし 連続する2つの偶数の2乗の差は4の倍数であることを証明しなさい。 J3 むつかしさB (ふつう) 連続する3つの奇数がある。 数の和に



中2数学 式の計算 文字式の利用 基本問題 問題 5 プリント



連続する3つの整数の和は3の倍数になるわけを説明しなさい 中学 Yahoo 知恵袋
1 連続する3つの整数について 2 偶数2mと奇数2n+1について, (1) 連続する3整数を,最小の数をnとするとして表しなさい。 n n+1 n+2 (1) 「偶数と奇数の和は奇数である」ことを,文字を使って説明しな・連続する三つの整数の和について考える。 思連続する三つの整数の和は,いつも3の倍数になっていること を,図や式,言葉を用いて論理的に考えている。 ・連続するいくつかの整数の和につい2=5 は整数より 5×(整数) の形となり、 連続する5 つの自然数の和は



令和3 21 年度用 中学校数学 内容解説資料a



Gakuto Co Jp Docs Download Pdf H28 Sugaku2 Seitoyoutest 2kaitou Pdf
よって、連続3項とも素数であるためには、初項pが3の倍数である素数、つまり3でなければならない。 (必要条件証明終わり) そこで、初項を3とすると、数列の値は、3 , 13 , 23 , 33 , である。 連続する3つの整数は,整数aを用いて, a,a1,a2 とあらわすことができる. その和は, a (a1) (a2)=3a3=3 (a1) となる.ここで, (a1)は整数であるから,3 (a1)は3の倍数である. よって,連続する3つの整数の和は3の倍数である. 連続する3つの整数の和の証明がわかる4ステップ 4ステップで証明できちゃうよ。 さっきの例題をといていこう! 連続する3つの整数の和が3の倍数になる訳を説明しなさい。 ただし、整数は正の数とする Step1 整数をnとする ある正の整数を「n」として




Akiya Su 中学数学 文字式の利用 標準レベルでは問題文のバリエーションは少ないので ワークなどでやりこむと良いでしょう 中学数学 文字と式 文字式の利用 整数



2
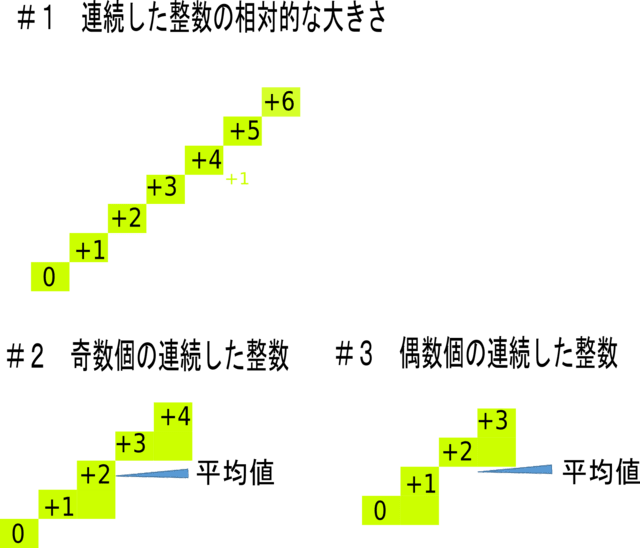
連続する5つの整数の和は たとえば 1つの場合として 1+2+3+4+5=15となり 15=5x3なので 5を3倍すると15になるので 5の倍数であることがわかります 5つの組み合わせすべての場合を確認するのはたいへんですは整数より 9×(整数) の形となり、 連続する3 つの3 の倍数の和は,9の倍数である 2 −整数 を用いて連続する5 つの自然数を −2、 1、 、 1、 2 と表せる。 よってその和は −2 ;+( − 1 ;とが求められる。連続する3つの自然数の和が3の倍数になることを示すため の式3(n+1)を,「連続する3つの自然数の中央の数n+1の3倍である」 とよみとることができるかどうかをみるものである。 中数B-3 太郎さんの説明



中学2年の数学です5つのつづいた整数のうち 中央の整数をnとし Yahoo 知恵袋



Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf
連続する3つの整数の積は6の倍数である. (証明) 連続する3つの整数の積を f(n) = (n 1)n(n1) とする.定理5 (1)よりf(n)が6 = 2 3の倍数であるためには,f(n)が2の倍数でもあ り,3の倍数でもあることを示せばよい.連続する3つには必ず偶数が含まれるので,明問1連続する3つの整数の和は3の倍数であることを,次のように文字式を使って説明しました。 にあてはまるものを書き入れましょう。 連続する3つの整数のうち,もっとも小さい整数をnとすると,連続する3つの整数は,n, , と表される。それらの和は,連続する3整数の積は 3!=6 の倍数 に 異なる n 個のものから m 個とってできる組合せの総数 n C m は整数であるが,順列・組合せの公式によれば n C m = =



連続する3つの整数について もっとも大きい数の2乗からもっと Yahoo 知恵袋



令和3 21 年度用 中学校数学 内容解説資料a
は整数だから, は3の倍数である。 したがって,連続する3つの整数の和は3の倍数である。 問2問1の説明で,連続する3つの整数の和が3(n1)と なることから,3の倍数であることのほかに,どんな ことがわかるでしょうか。 問32桁の自然数と,その十の位の数(5) 62×91+38×91 (6) 314×75-314×25 3《整数の性質を調べる》次の各問いに答えよ。 (1) 差が2 である2 つの整数の積に1 をたすと,ある整数の2 乗にな ることを証明せよ。 (2) 連続する2 つの奇数の積と大きい方の奇数を2 倍した数の和は,例題 連続する \(3\) つの整数の和は、\(3\) の倍数になることを、文字を使って説明しなさい。 解説 初めてこの問題を見て、何がなんやらポカーンとなっているみなさん。 大丈夫です。 一からしっかりと解説をしていき




この問題が分かりません よかったら回答お願いします 問題多くてすみません Clear




3times 6right 33 N Descubre Como Resolverlo En Qanda




中学数学 式による説明 のコツと練習問題




なぜ N 1 N N 1ではないのですか Clear



高校数学 連続する3つの整数の積は6の倍数である を利用する問題 特に の Yahoo 知恵袋




連続した5つの整数の和は5の倍数 もののはじめblog



連続する3つの整数の和は 3の倍数になる そのわけを説明しなさい と言 Yahoo 知恵袋



数学 整数や自然数を文字式であらわすには



Http Www Wakayama Edc Big U Jp Toutatudo H26tobun Jss Pdf




数学 中2 9 文字式の利用 基本編 Youtube




高校数学b 等差数列を利用する倍数の和 受験の月



Http Www Wakayama Edc Big U Jp Toutatudo H26tobun Jss Pdf




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




中2数学no 16 式の説明 連続する3つの整数の和は3の倍数になる Youtube
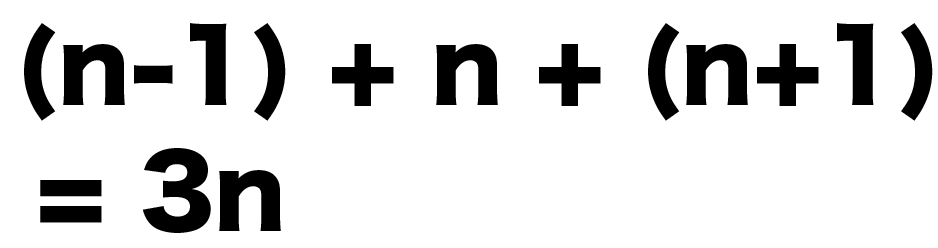



文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




Okra Newmathworkbook Twitter



Http Www News Ed Jp Gimu Yumeako Gakuryoku H19 H19cyusu H19cyusub 2 Pdf



2




無料 中2数学 基本問題 解答プリント 6 式の計算6 等式の変形



Core Ac Uk Download Pdf Pdf



Http Xavier Ed Jp Wp Wp Content Uploads 05 aad4ee3144fc029c51 Pdf




高校数学a 連続する整数の積 の性質 映像授業のtry It トライイット




連続する3つの整数の和 Youtube



3 4 5や5 6 7のような奇数から始まる連続する3つの整数の和は6 Yahoo 知恵袋



3つの続いた整数の和は 3の倍数になることを説明しなさい の問題 Yahoo 知恵袋



整数の性質の説明2 チーム エン




1 1 3 3 Descubre Como Resolverlo En Qanda




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




赤点脱出シリーズ 捨てている人 損です 式による説明問題の解き方 コツさえ分かれば楽勝 夏期講習 生駒市 奈良市の個人契約 家庭教師しゅ 先生




P27 2 1 N Lihat Cara Penyelesaian Di Qanda



1



Core Ac Uk Download Pdf Pdf




学校で文字式の利用 連続する整数 2けたの正の整数 について勉強しているが 全然わか Clear




電気磁気工学を学ぶ 17



Www Moka Tcg Ed Jp Nakajhsc Wysiwyg File Download 1 4939




連続する3つの整数の積が6の倍数であることの証明 タロウ岩井の数学と英語 Note




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




この問題が分かりません よかったら回答お願いします 問題多くてすみません Clear



3つの続いた整数では それら3つの整数の積に中央の整数を加えると 中央の整数の Yahoo 知恵袋




3times 6right 33 N Descubre Como Resolverlo En Qanda




中学数学2年 文字式の利用 整数の性質 受験の月



Www City Funabashi Lg Jp Gakkou 0002 Asahi J 0003 P0798 D Fil 4 1 Pdf




2次方程式の文章問題 自然数や整数を求める問題 バカでもわかる 中学数学



3つの連続した偶数の整数の合計 Sioghesber1



連続する3つの整数の和は 3の倍数になる そのわけを説明しなさい と言 Yahoo 知恵袋



連続する3つの整数の和は3の倍数になるわけを説明しなさい 中学 Yahoo 知恵袋




今日の授業内容です 何一つ理解できませんでした 教えてほしいです Clear




連続する3つの奇数の和は3の倍数になることの説明 中学数学 講義 Youtube



連続する3つの奇数の和は3の倍数になることを説明せよ と真剣に向き合う 風の貌 かぜのかたち




整数についての証明 3つの連続する偶数 Youtube




Akiya Su 中学数学 文字式の利用 標準レベルでは問題文のバリエーションは少ないので ワークなどでやりこむと良いでしょう 中学数学 文字と式 文字式の利用 整数




高校数学a 連続する整数の積 の性質 練習編 映像授業のtry It トライイット




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




連続する3つの自然数の3乗の和は9の倍数であるか Ameblo Hacks アメブロを10倍楽しむために努力するブログ




赤点脱出シリーズ 捨てている人 損です 式による説明問題の解き方 コツさえ分かれば楽勝 夏期講習 生駒市 奈良市の個人契約 家庭教師しゅ 先生



Www Nier Go Jp Tyousakekka Tyousamondai Kaisetsu Kaitou Chuu Suugaku B2 Renzoku Sizensuu Pdf



数学文字式の利用 連続する5つの整数の和は5の倍数であることを 文字式を使 Yahoo 知恵袋




高校数学a 3の倍数 9の倍数の見分け方 映像授業のtry It トライイット




電気磁気工学を学ぶ 17



Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf



3つの続いた整数の和は 3の倍数になることを説明しなさい の問題 Yahoo 知恵袋



2



Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf




連続n整数の積は何の倍数 数学の偏差値を上げて合格を目指す




5 12 1314 39 3 3 3 4 R Descubre Como Resolverlo En Qanda



1




1 2 Descubre Como Resolverlo En Qanda




1 3 3 Descubre Como Resolverlo En Qanda




高校数学b 階差を利用する和 連続整数の積の和 Sk K 1 K 2 受験の月




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座




無料 中2数学 テスト対策 解答プリント 3 式の計算3 利用




高校 数学a 整数25 連続する整数の積 13分 Youtube



令和3 21 年度用 中学校数学 内容解説資料a



Media Toriaez Jp Q08 8 Pdf



5hmetwzt Zx8lm




連続する3つの自然数の積と倍数 不定方程式の応用 2019センター試験 数学 a 第4問 選択 テンメイのrun bike




これって整数をnとして計算してもいいですか Clear



2



2




数学 整数や自然数を文字式であらわすには



文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく



連続する3つの整数の和は 3の倍数になる そのわけを説明しなさい と言 Yahoo 知恵袋




1枚目と2枚目の問題はほぼ同じような問題だと思うのですが 2枚目の問題は1枚目の問題 Clear




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく



連続する3つの整数のうち中央の数をnとすると 残りのふたつの数はそれぞ Yahoo 知恵袋



0 件のコメント:
コメントを投稿