円に内接する四角形の外角は,対角 (内角)に等しい。 → a の外角は c の角度と同じ。垂心の性質《証明》 三角形の垂心がもつ性質の証明をします。 まずは「 四角形adhf,behd,cfheは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。 2円の位置関係は,\ 以下の\textbf {\textcolor {purple} {5パターンに分類}}される \\2円の半径と中心間の距離の関係}}によって分類される 離れている {外接する {2点で交わる}内接する {一方が他方の内部にある \hspace {5zw}この2円の位置関係を調べよ 原点と (x_1,\ y_1
1
円の性質 日常
円の性質 日常-中学3年生 数学 円の性質の利用 練習問題プリント 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習指導要領(21年度全面実施)への対応作業を進めておりますが、 現在のところ円に内接する四角形の性質について考えてみよう。 円に内接する四角形 定理 円に内接する四角形では,次の1, 2 が成り立つ。 1 対角の和は 180° である。 2 外角は,それと隣り合う内角の対角 に




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
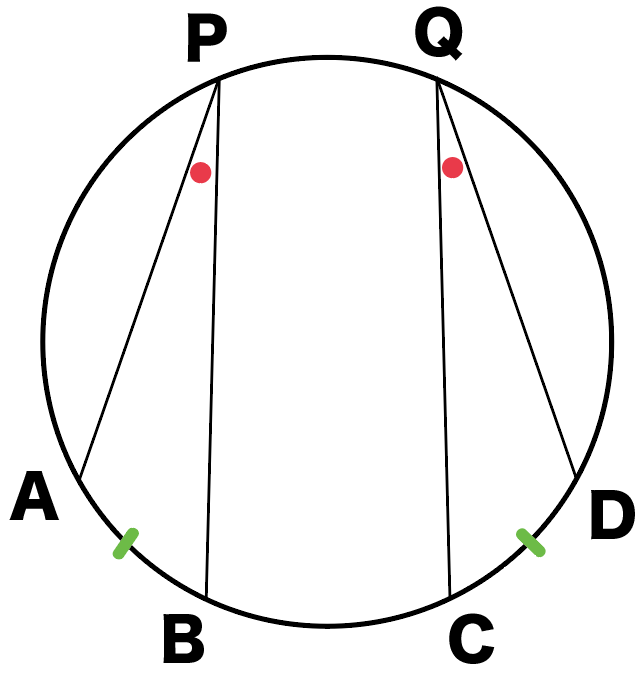
中学 数量 正負の数(加法) 正負の数(減法) 正負の数(乗法) 正負の数(除法) 平方根を裁ち合わせで 面積が3の正方形 対称な図形 線対称な図形 点対称な図形 その2 対称移動 回転移動 平行移動と対称移動 平行移動と回転そして、これらの性質についての解説も行います。 円とは はじめに円の定義から始めます。 円とは、ある点との距離が等しくなる点の集合である。 このある点のことを円の中心と呼ぶ。 集合で書くと中心が原点で半径 の円は以下のようになります。逆に、「直角三角形の各頂点を通る円は、斜辺(直角に対する辺)がその円の直径になる」というのも重要な性質です。 円周角の定理の逆 図のように 「点a、点b、点p、点qにおいて、∠apq=∠aqbなら、すべての点は1つの円周上にある」 といえます。
最後に外心、内心、重心のポイントをまとめておきましょう。 外心 3辺の垂直二等分線が交わる点 各頂点から等しい距離にある 各頂点から線を結ぶと二等辺三角形ができるので、底角が等しい 円周角の定理が使える 内心 3つの角の二等分線が円の性質 三角形や多角形の事を学んだら次は円に移る。 円というのは非常に単純な形であるが様々な性質がある。それを一つ一つ見ていこう。 ちなみにこれからあげる円の性質は「一つの円において」または「同じ大きさの円において」考 円の性質を基に,よく回るこまの条件について説明している。 関 円や弧のもつ美しさに気付き,進んで模様づくりをすることが できる。 3 単元構想図(単元計画と評価) 本単元の学習の流れ(全10時間) 課題の設定 整理・分析
内接円の性質 内接円には、大きく \(2\) つの性質があります。 性質①内心と各辺の距離 多角形のそれぞれの辺が内接円の接線となっていて、各接点から引いた垂線の交点が内接円の中心(内心)となります。 いよいよ、円の性質っていう単元を勉強していくよ。 今日は、この単元でいちばん大事な、円周角の定理とはなにか??をまとめてみたんだ。計算や証明で使ったりするから、しっかりおさえてあげてね。 = もくじ = 円周角・中心角とは? 性質1の逆も成立します。つまり, 向かい合う内角の和が 18 0 ∘ 180^{\circ} 18 0 ∘ である四角形は円に内接します。 また,性質1は「外角」を使って表現されることも多いです。




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
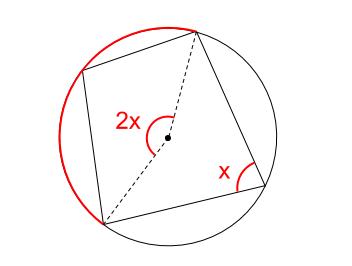



円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su
円に内接する四角形の性質まとめ対角の和が180°になる理由 Tooda Yuuto 18年8月22日 / 19年9月9日 四角形の つの頂点 がすべて同じ円周上にある(内側から接している)とき、「四角形 は円に内接する」といいます。 反対に、四角形 の つの辺がすべて円の性質のまとめ ここで4点が同一円周上のあるための条件,直線が円の接線になるための条件に注目して 円の性質をまとめておきます. なお,証明は,最後のトレミーの定理以外,すでに学んだページを参考にして下さい. 命題 四角形abcdで次が成り立つ.円と直線が同一平面状に存在するときには, ・ 2 点で交わる ・ 接する ・ 離れている の 3 つの場合が考えられます。 ここでは接するときを考えていきます。 円に接する直線のことを円の接線といいます。 また,このときただ 1 つの共有点のことを接点 といいます。




円の性質の利用 チーム エン
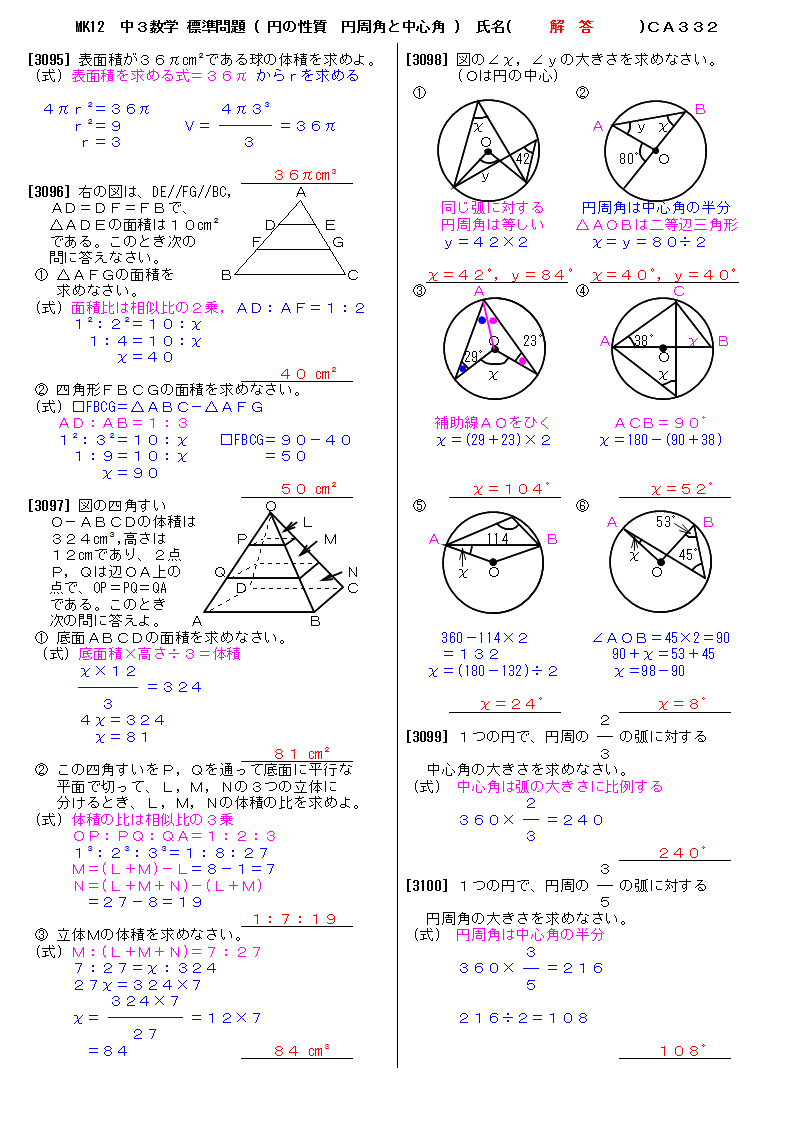



無料 中3数学 標準問題 解答プリント 332 円の性質 円周角と中心角
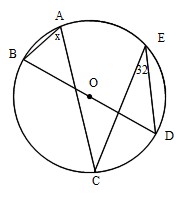
② 円の外の 1 点から 2 本の直線が円とそれぞれ異なる 2 点で交わるとき このとき, が成り立ちます。 このことは以下のように証明することができます。 と において, 共通な角なので, 内接四角形の性質より, よって,右の図のような円があり,異なる3点 a, b, c は円周上の点である。線分 ac 上に,2点 a, c と異なる点 d をとる。また,2点 b, d を通る直線と円との交点のうち,点 b と異なる点を e とする。 ∠ abe=35°, ∠ cde=80° であるとき, ∠ bec の大きさは何度か。内心と傍心のどちらも "角の2等分線の交点" なので似たような性質を持ちます。 その性質のひとつを紹介します。 内心は三角形の内接円の中心の点です。 三角形の面積を\(S\)、内接円の半径を\(r\)とすると \S=\displaystyle \frac {1}{2} r(abc)\ が成り立ちます。
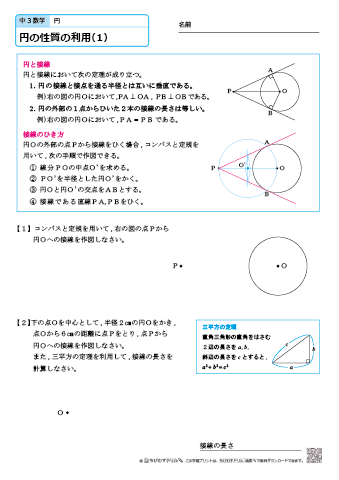



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット
円と直線 三角形と円 接線の長さ 2円の位置関係 2円の共通接線 同じ弧に対する円周角 円周角の定理の逆 円に内接する四角形円と球 小学3年生の円と球プリントです。 こちらのプリントでは一部コンパスを使用した作図問題があります。 正確な長さを作図する能力が求められますので、 必ず100%の比率で印刷(倍等印刷)して下さい。 そうしないと1cm角のマス目が08cm角など中途内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離




中3数学 円の性質17 円の性質を利用した証明 すべて無料 星組の中学数学講座




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット
円と接線に関する3定理(垂直、接線の長さ、接弦定理) スポンサーリンク 高校数学A 平面図形 検索用コード 円の接線は,\ 接点を通る半径と垂直をなす 円の外部の点から引いた2本の接線の長さは等しい 接点を通る弦と接線が作る角は,\ その角MathAquarium練習問題図形の性質 14 14 次の図において,x の値を求めよ。ただし,(3)の直線PT は接点をT とする円の接線である。 (1) (2) (3) Px A 9 D C 5 P B8 6 A D 4 C B x 3 2 P A T B x三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出
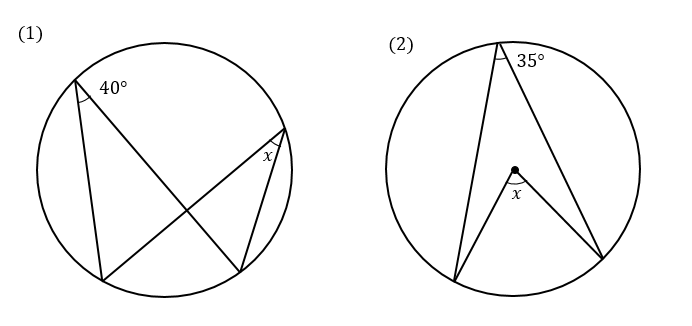



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
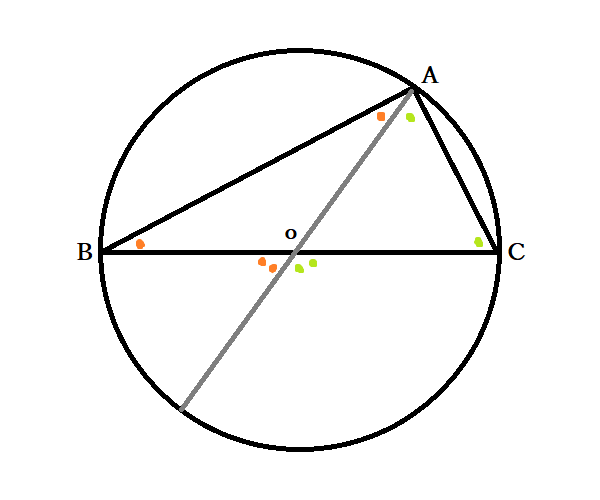
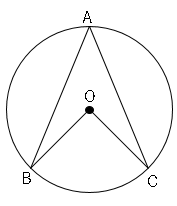
円の性質 っていう単元 を勉強していくよ。 今日は、この単元でいちばん大事な、 円周角の定理とはなにか?? をまとめてみたんだ。 計算や証明で使ったりするから、しっかりおさえてあげてね。 = もくじ = 円周角・中心角とは?? 円周角の定理とは?続いて図2のように、円の中心Oを1つの頂点とする OABがあるとします。 点OからABに垂線を下ろしその交点をMとしたとき、OMはABを2等分する線になります。 逆を言えば、弦ABの垂直二等分線は、必ず円の中心を通ることになります。 ・外接円をもつ四角形の性質円に内接する四角形の性質 1:円に内接する四角形の対角の和は180° 2:四角形の内角は、その対角の外角に等しい ※ 「円に内接する四角形の対角の和は180°」定理の証明




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



中学校数学 証明のコツ 入試問題 円




円周角の定理 円に内接する四角形の性質 分かりません 教えてください Clear



3



Studydoctor円に内接する四角形の性質 中学3年数学 Studydoctor




数学a基礎 図形の性質 解説 例題コース 最新刊 無料試し読みなら漫画 マンガ 電子書籍のコミックシーモア




円の性質 円周角 図形 数学 高校受験講座 東京先生



円の性質 数学の要点まとめ 練習問題一覧



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
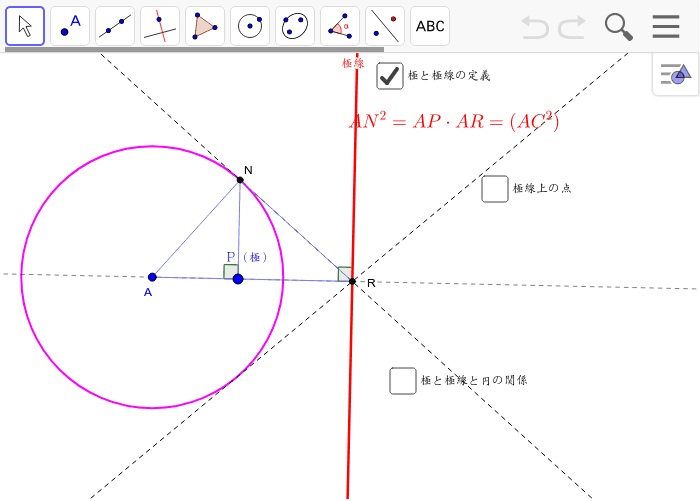



円の極と極線の性質 Geogebra
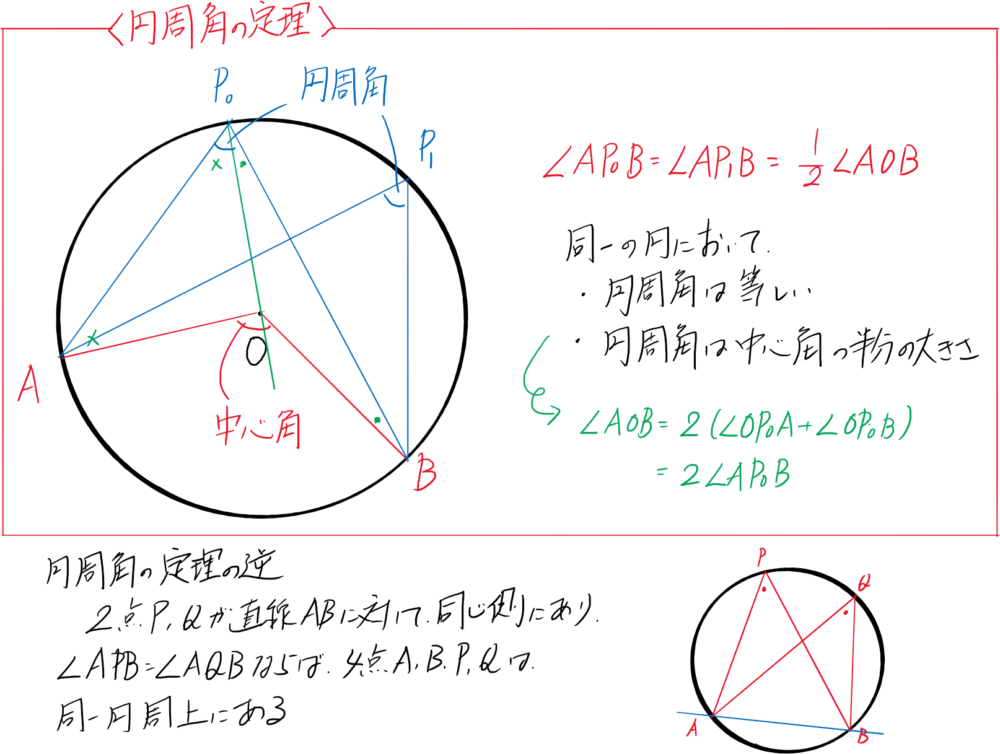



円の性質 円周角の定理 平面幾何 富岡市の総合学習塾 トータルアカデミー
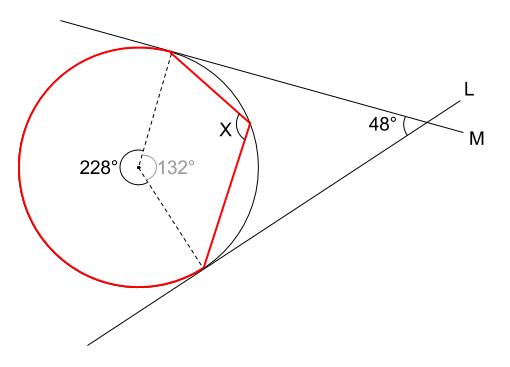



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su
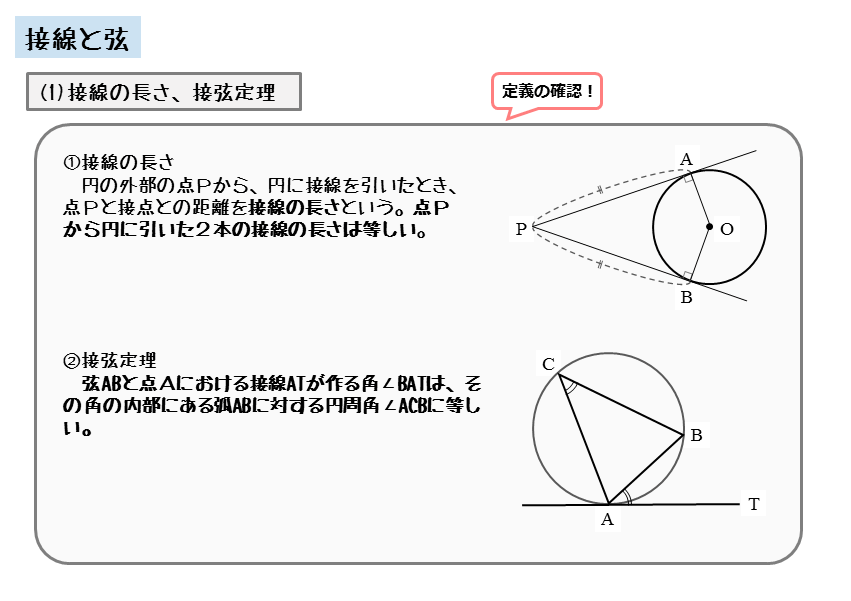



図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん



1



円の性質 数学の要点まとめ 練習問題一覧



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく




公立入試問題の解説 円の性質 桃李塾のブログ
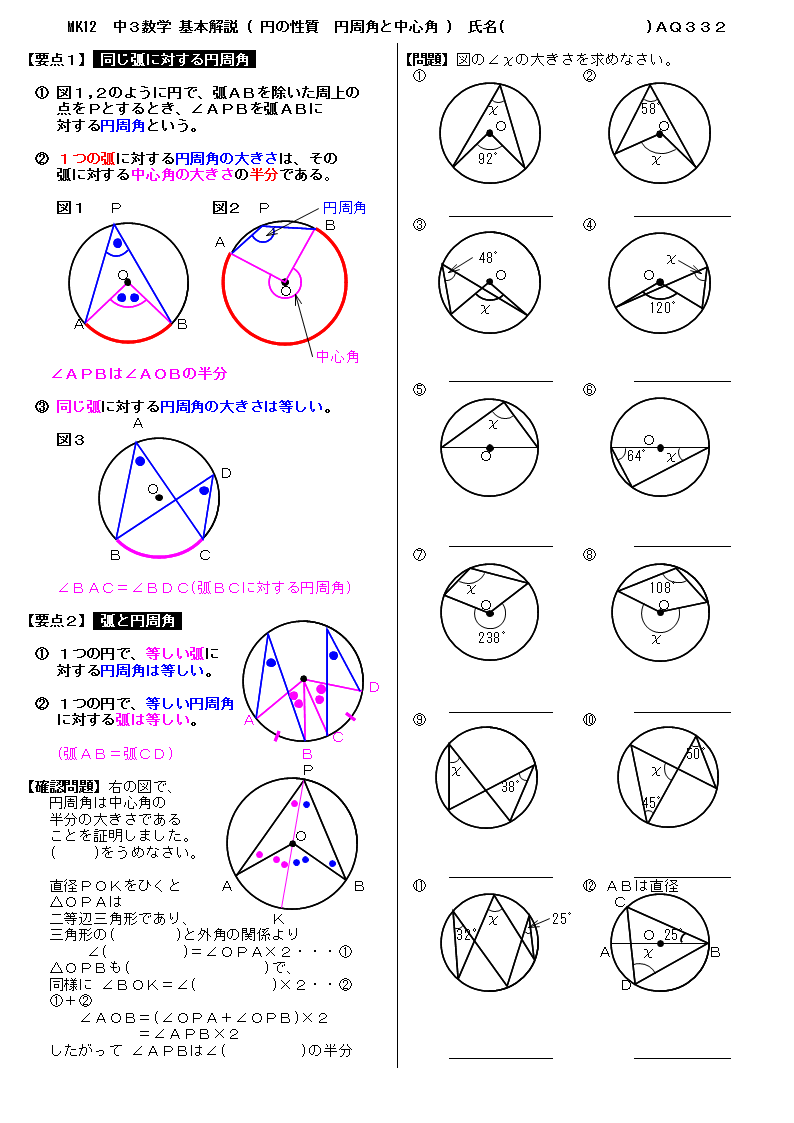



無料 中3数学 基本解説 問題プリント 332 円の性質 円周角と中心角




円の性質と円の条件 感じる科学 味わう数学




三角形の外接円の 4 つの性質 証明付 理数アラカルト




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



2




中3 中3 円周角の定理 円の性質の利用 中学生 数学のノート Clear




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




中3数学 円の性質12 接線と弦のつくる角 接弦定理 すべて無料 星組の中学数学講座




中3数学 円の性質3 円周角と中心角 すべて無料 星組の中学数学講座




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
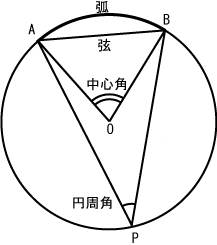



円 数学 Wikipedia




高校数学a 円周角と中心角のおさらい 例題編 映像授業のtry It トライイット
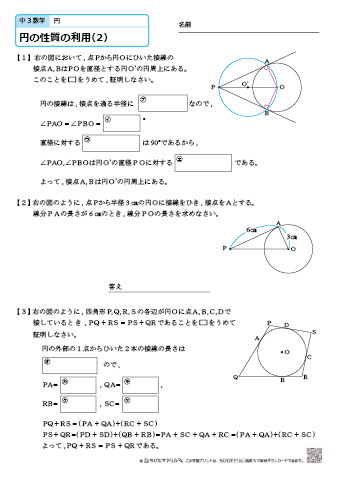



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
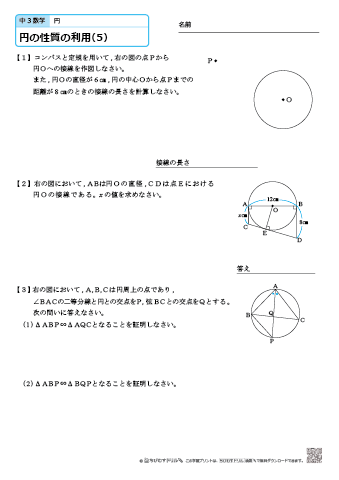



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
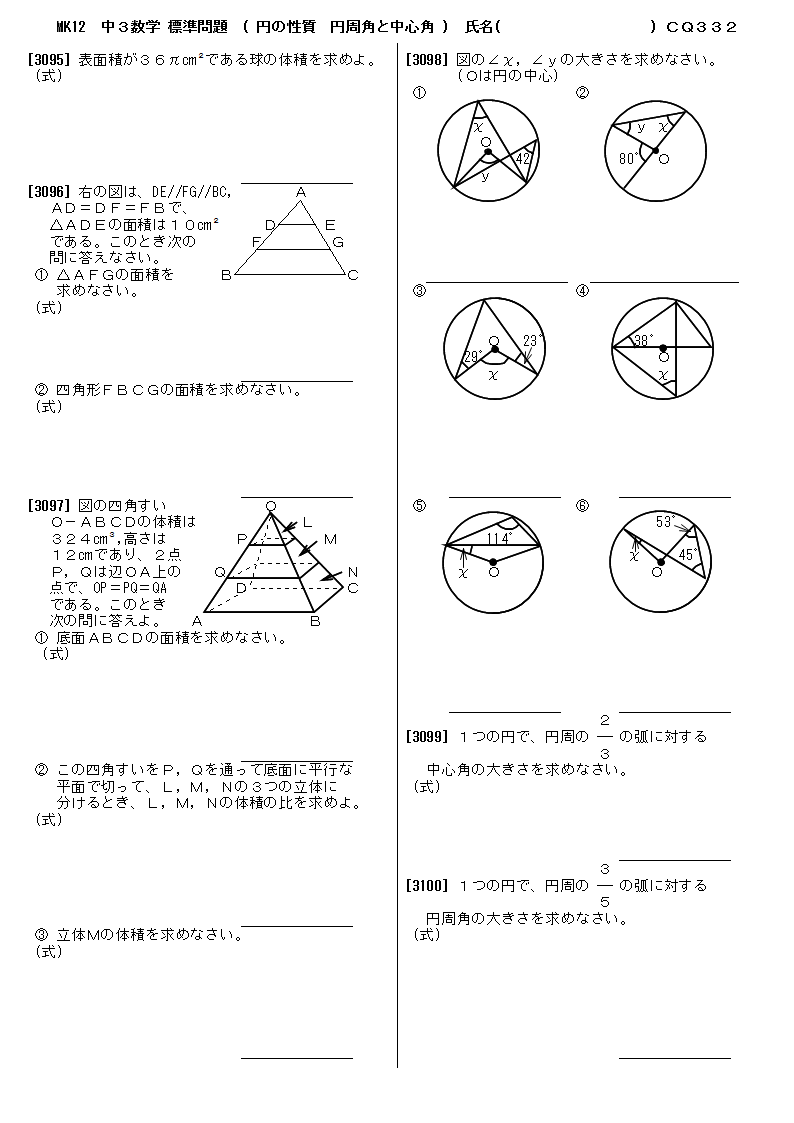



無料 中3数学 標準問題 問題プリント 332 円の性質 円周角と中心角
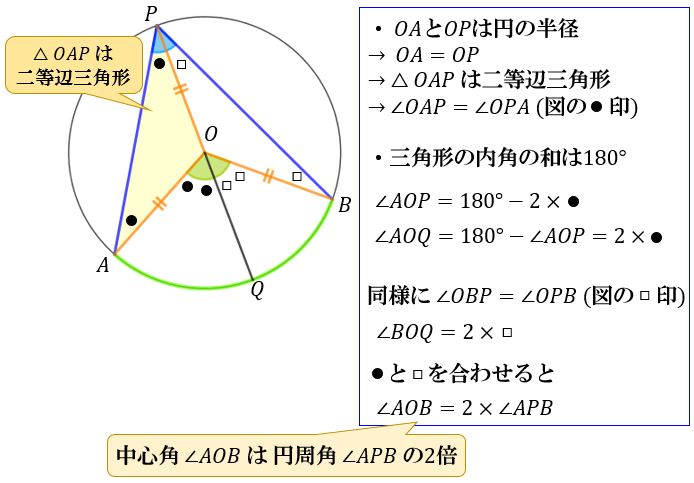



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
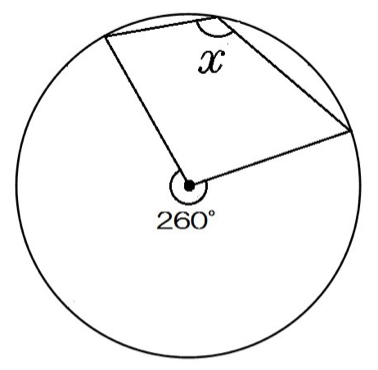



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



数学a 平面図形 円の性質 円の接線
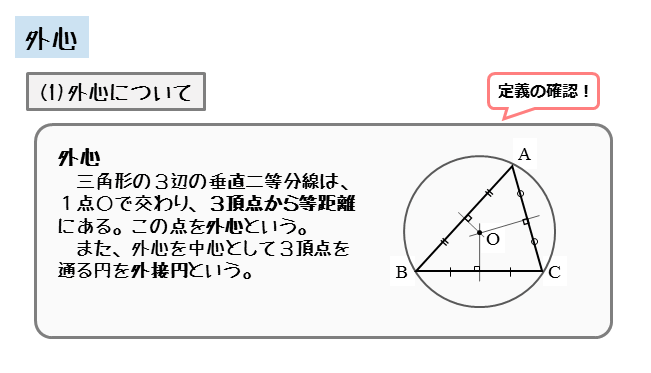



図形の性質 外心について 日々是鍛錬 ひびこれたんれん
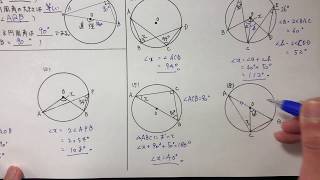



中3数学 円の性質2 円周角と中心角 すべて無料 星組の中学数学講座
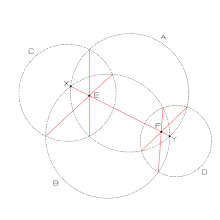



円 数学 Wikipedia
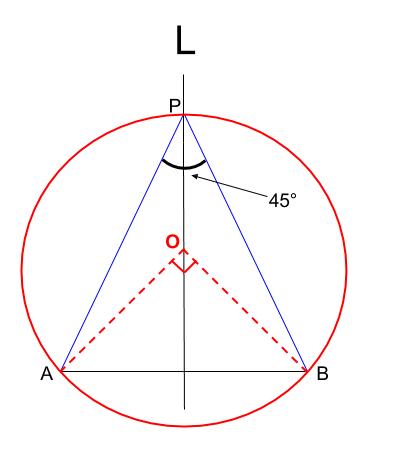



45 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su



Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data A 319 A Shinsugaku 319 A Kyoukashopdf 319 A Kyoukashopdf 2 2 Pdf



1
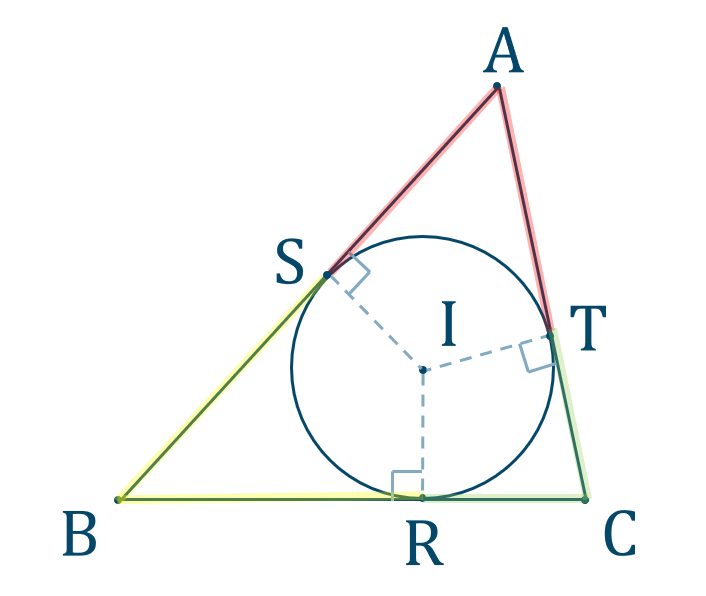



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学
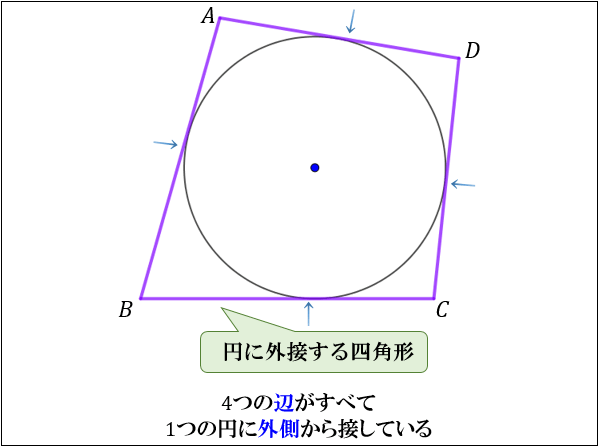



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ
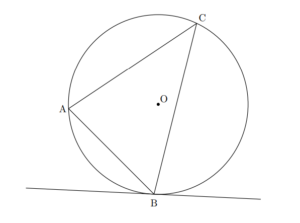



円に関する性質その1 接弦定理 高校数学の知識庫




中学数学 円と接線 Youtube




数学a基礎 図形の性質 演習コース 数学a基礎 演習コース 石井大裕 数学 Kindleストア Amazon
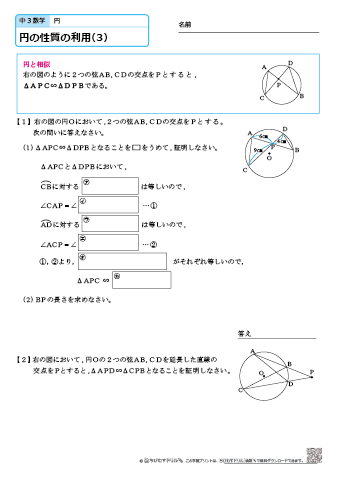



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
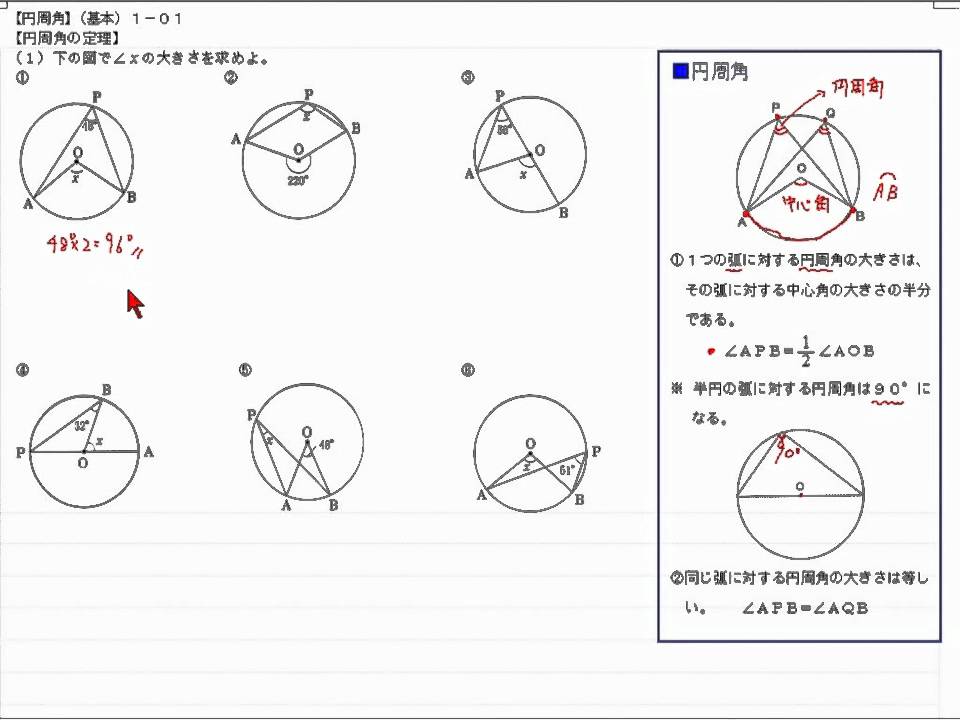



No 295 中3数 円の性質 円周角 基本 1 01 ネット塾の英進塾 Youtube




図形の性質がわかません 図の Oebが90度になる理由がわかりません Okwave
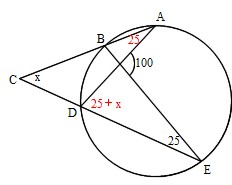



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
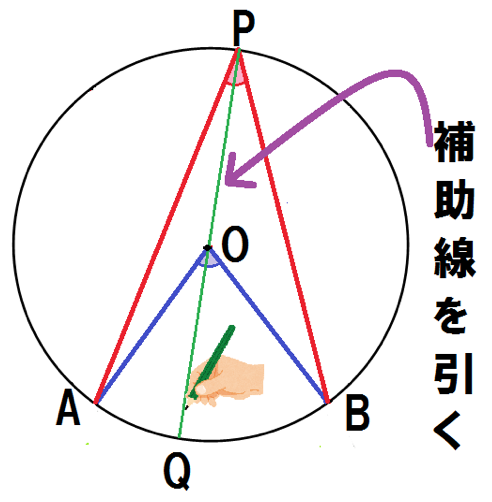



円の性質 Qikeru 学びを楽しくわかりやすく




中3数学 円の性質16 円の性質を利用した証明 Youtube



数学a 平面図形 円の性質 方べきの定理




中学 高校までの円に関する定理や性質をまとめました 平面図形 高校生 数学のノート Clear
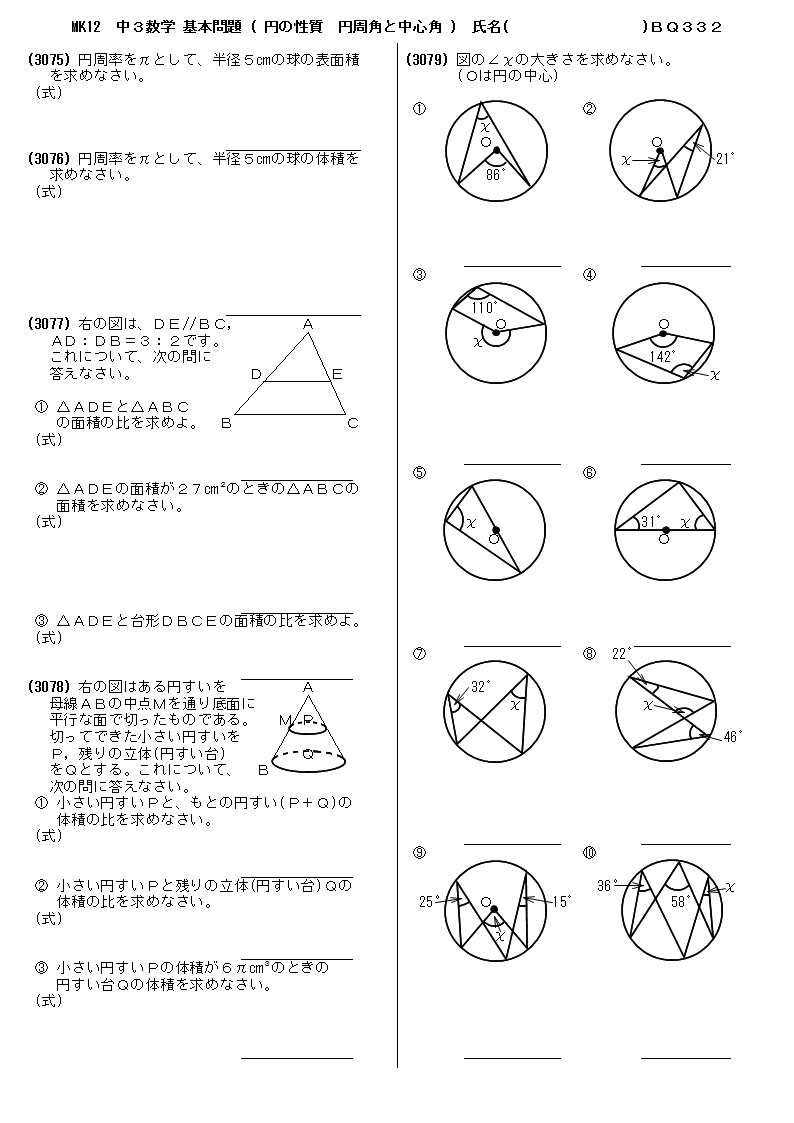



無料 中3数学 基本問題 問題プリント 332 円の性質 円周角と中心角
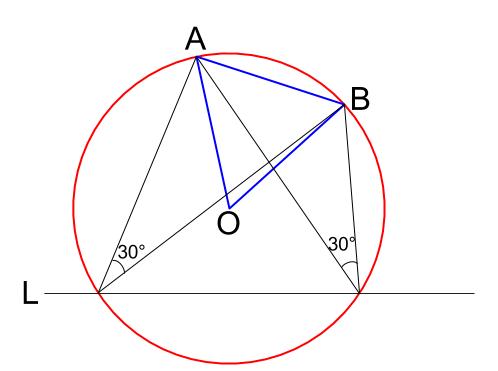



30 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



2




角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ
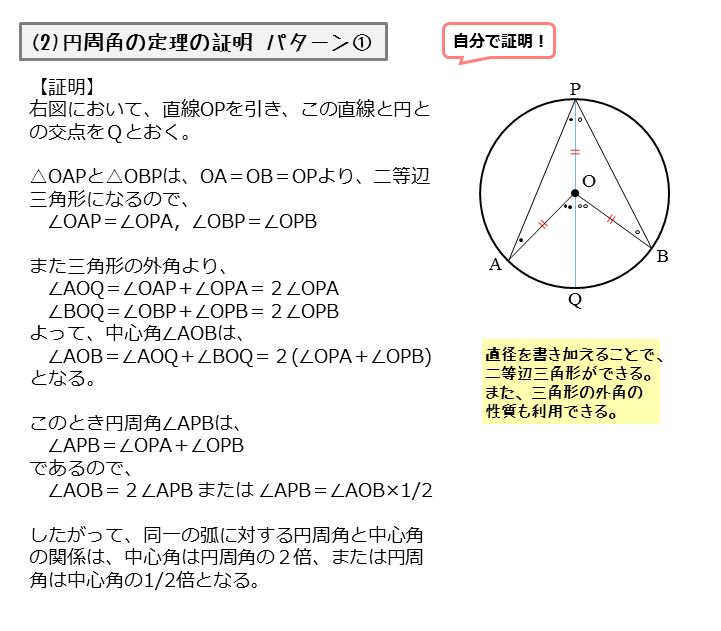



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん



1




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
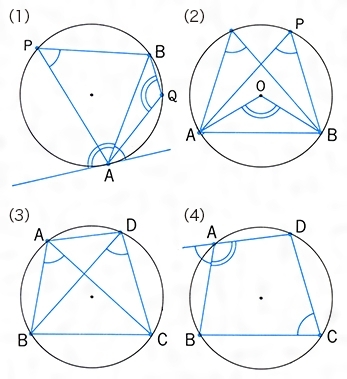



円周角とは コトバンク
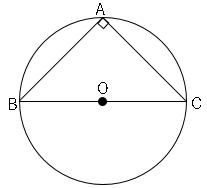



円の性質 数学の要点まとめ 練習問題一覧




7講 円と直線 1節 平面図形 問題集 2章 図形の性質
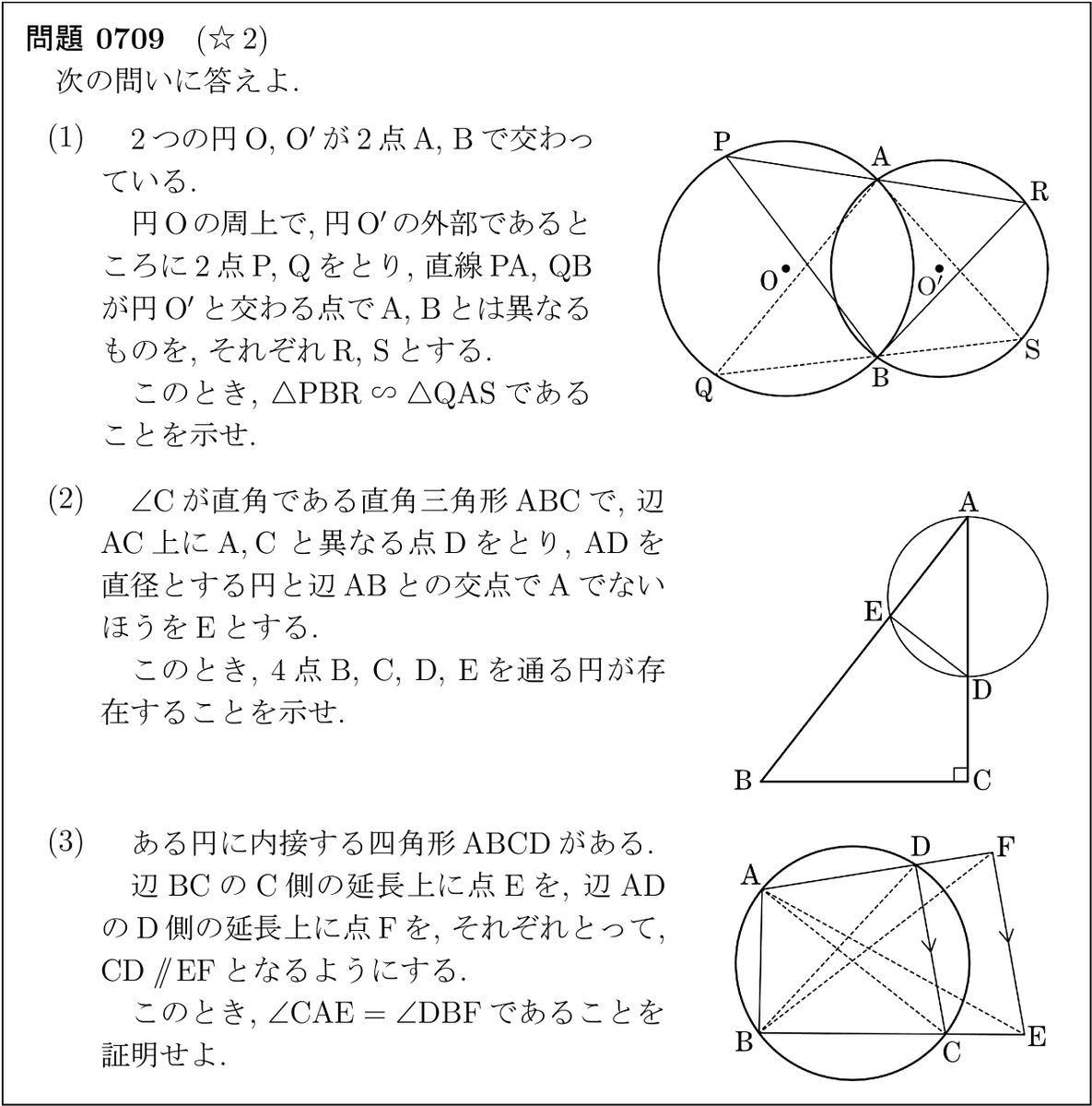



高校数学基本問題垂れ流し Ar Twitter 07 図形の性質 2 円 円周角 円に内接する四角形 4点が同一円周上にある条件と証明




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット
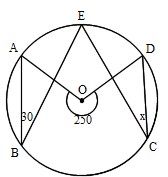



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
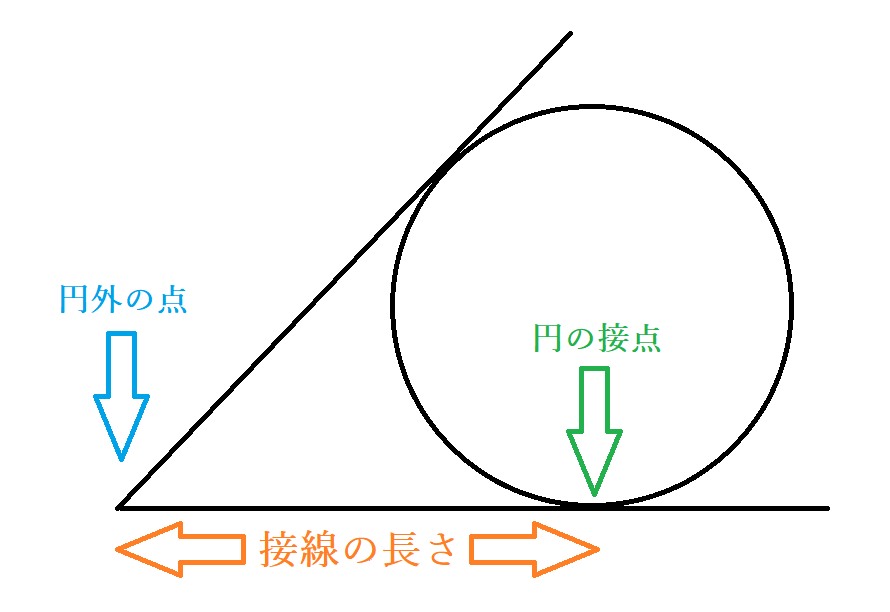



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog




中学生 円の性質のノート一覧 Clear




円周角の定理の逆 中学3年生 円の性質 数学 Youtube




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



外接円とは 半径の公式や求め方 性質 書き方 受験辞典
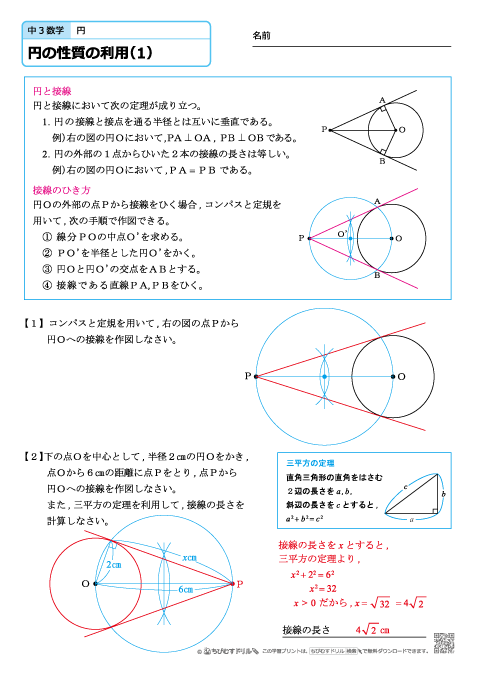



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
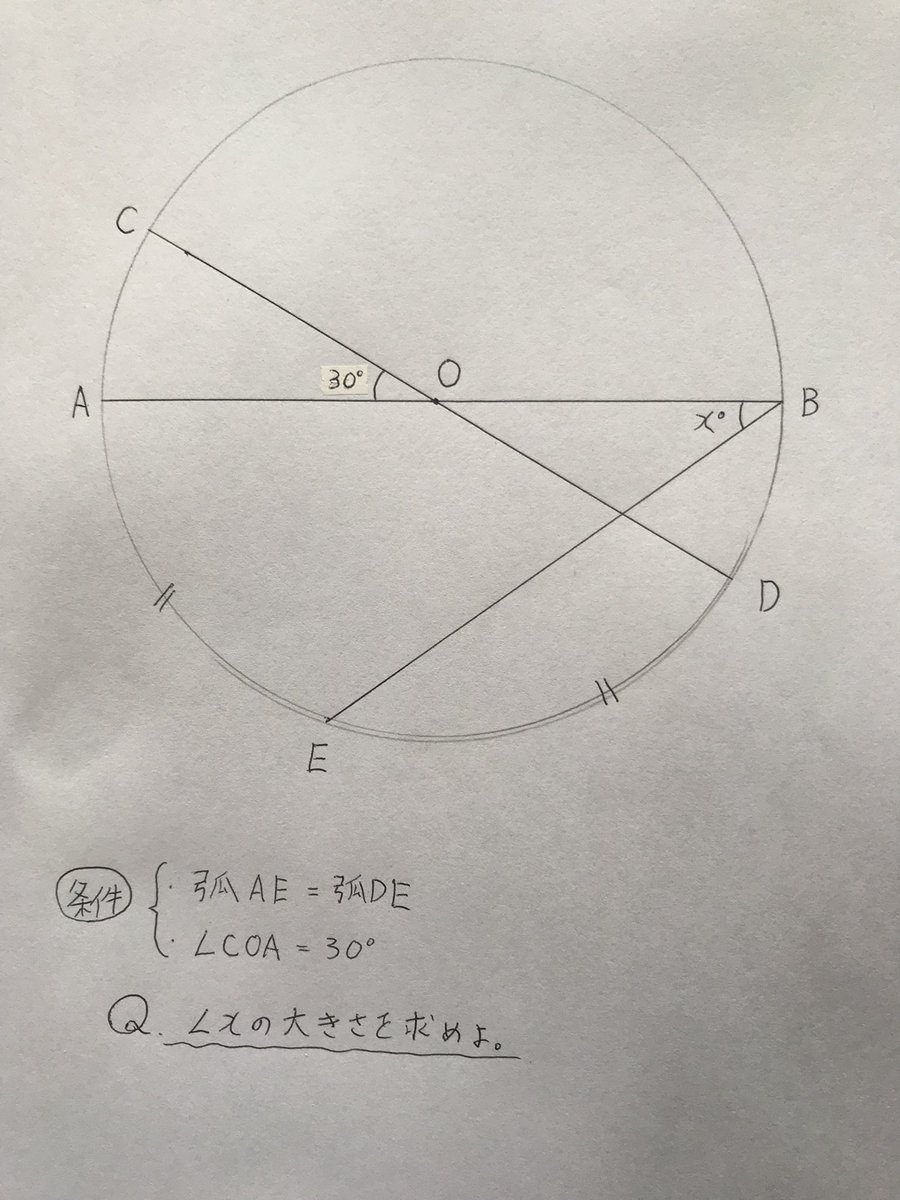



円の性質




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




世界一わかりやすい数学問題集中3 6章 円の性質
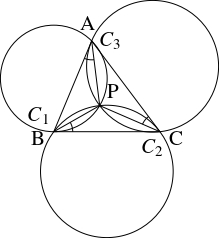



円の性質




図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
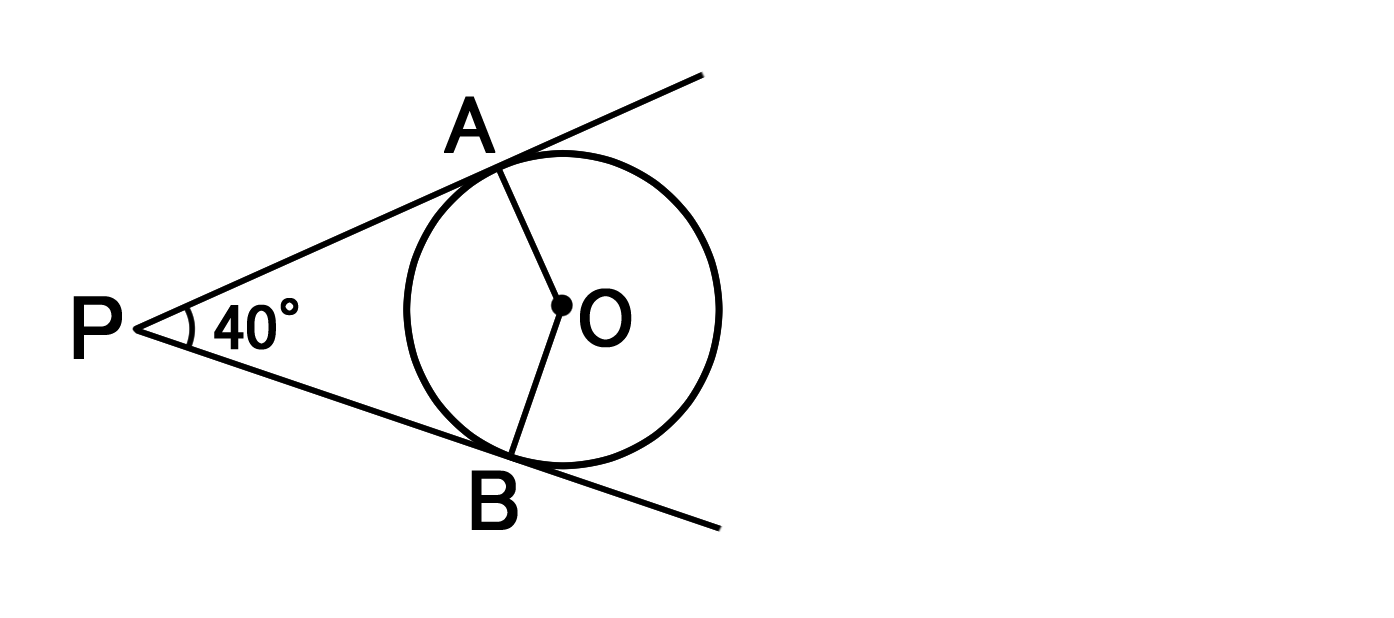



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学



中3数学 円の性質1 円周角と中心角 証明 すべて無料 星組の中学数学講座
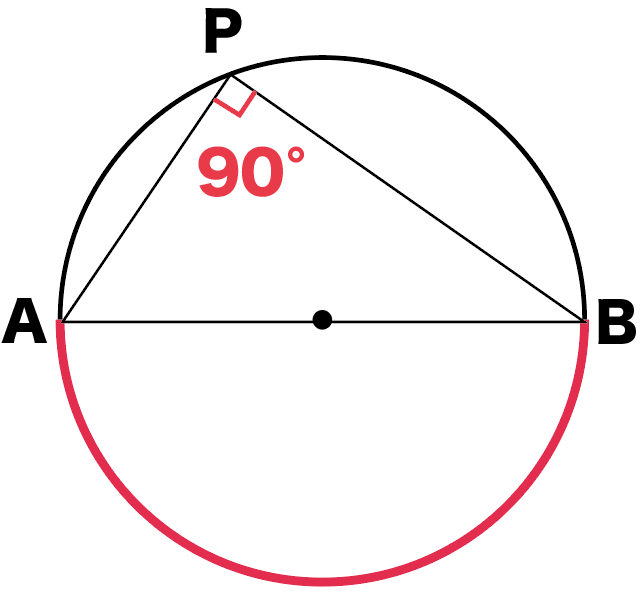



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく




โน ตของ 数a 図形の性質 要点まとめ 円編 ช น Senior Clear



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




円の中心角 弧 弦 Jsciencer
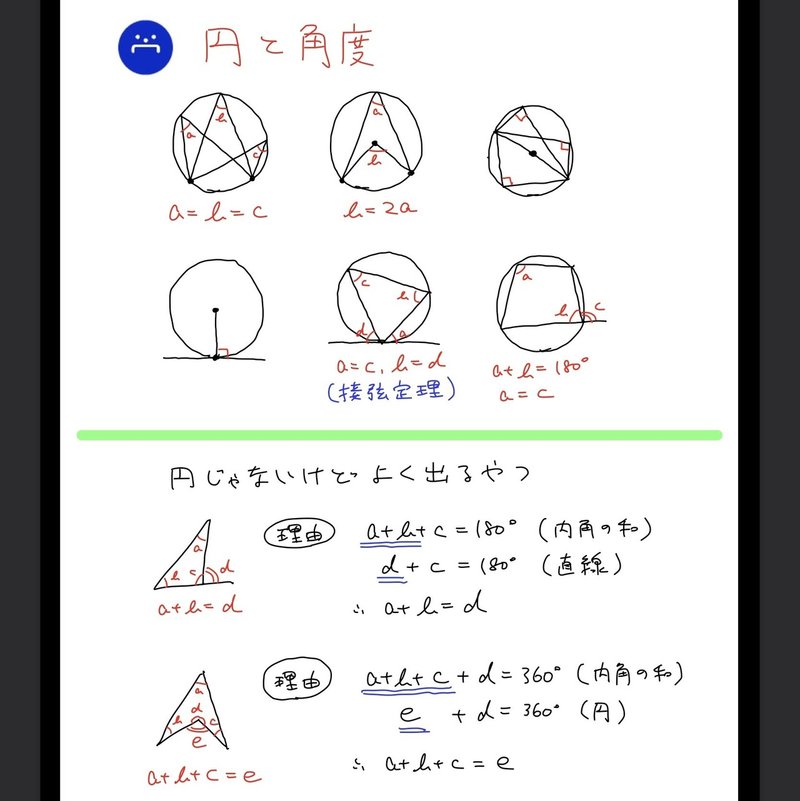



高校数学無料問題集 数a 第2章 図形の性質 円に関する問題 桝 ます Note
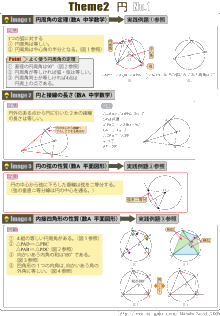



円 に関するチャートを作ってみました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



円の性質 数学の要点まとめ 練習問題一覧



0 件のコメント:
コメントを投稿